Calculus

Show Mobile Notice

Calculus definition is - a method of computation or calculation in a special notation (as of logic or symbolic logic). How to use calculus in a sentence. Calculus is an area of math that deals with change. It has two main parts: Differential and Integral Calculus. Differential Calculus is based on rates of change (slopes and speed). Integral Calculus is based on accumulation of values (areas and accumulated change). Both parts of calculus are based on the concept of the limit. Here is a set of notes used by Paul Dawkins to teach his Calculus I course at Lamar University. Included are detailed discussions of Limits (Properties, Computing, One-sided, Limits at Infinity, Continuity), Derivatives (Basic Formulas, Product/Quotient/Chain Rules L'Hospitals Rule, Increasing/Decreasing/Concave Up/Concave Down, Related Rates, Optimization) and basic Integrals (Basic Formulas. Calculus is the branch of mathematics that deals with continuous change. Calculus is also called infinitesimal calculus or “the calculus of infinitesimals”. Classical calculus is the study of continuous change of functions. The two major concepts of calculus are derivatives and integrals. One of the foremost branches of mathematics is calculus. The formal study of calculus started from the 17th century by well-known scientists and mathematicians like Isaac Newton and Gottfried Leibniz, although it is possible that it has been at use as early as the Greek era.

Show All Notes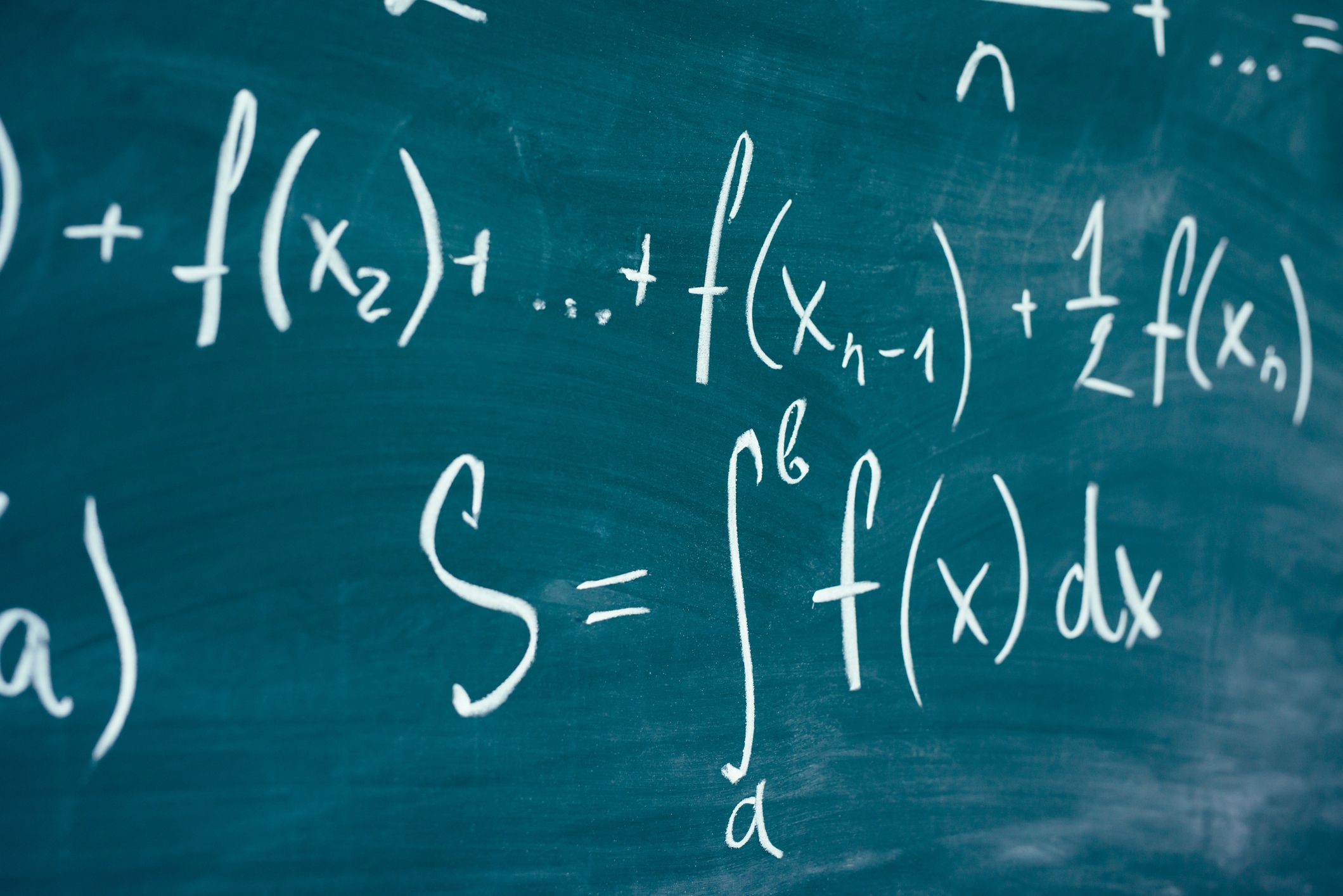

Hide All Notes

You appear to be on a device with a 'narrow' screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.

Here are a set of practice problems for the Calculus I notes. Click on the 'Solution' link for each problem to go to the page containing the solution.

Note that some sections will have more problems than others and some will have more or less of a variety of problems. Most sections should have a range of difficulty levels in the problems although this will vary from section to section.

Here is a listing of sections for which practice problems have been written as well as a brief description of the material covered in the notes for that particular section.

Review - In this chapter we give a brief review of selected topics from Algebra and Trig that are vital to surviving a Calculus course. Included are Functions, Trig Functions, Solving Trig Equations and Equations, Exponential/Logarithm Functions and Solving Exponential/Logarithm Equations.

Functions – In this section we will cover function notation/evaluation, determining the domain and range of a function and function composition.
Inverse Functions – In this section we will define an inverse function and the notation used for inverse functions. We will also discuss the process for finding an inverse function.
Trig Functions – In this section we will give a quick review of trig functions. We will cover the basic notation, relationship between the trig functions, the right triangle definition of the trig functions. We will also cover evaluation of trig functions as well as the unit circle (one of the most important ideas from a trig class!) and how it can be used to evaluate trig functions.
Solving Trig Equations – In this section we will discuss how to solve trig equations. The answers to the equations in this section will all be one of the “standard” angles that most students have memorized after a trig class. However, the process used here can be used for any answer regardless of it being one of the standard angles or not.
Solving Trig Equations with Calculators, Part I – In this section we will discuss solving trig equations when the answer will (generally) require the use of a calculator (i.e. they aren’t one of the standard angles). Note however, the process used here is identical to that for when the answer is one of the standard angles. The only difference is that the answers in here can be a little messy due to the need of a calculator. Included is a brief discussion of inverse trig functions.
Solving Trig Equations with Calculators, Part II – In this section we will continue our discussion of solving trig equations when a calculator is needed to get the answer. The equations in this section tend to be a little trickier than the 'normal' trig equation and are not always covered in a trig class.
Exponential Functions –In this section we will discuss exponential functions. We will cover the basic definition of an exponential function, the natural exponential function, i.e. ({bf e}^{x}), as well as the properties and graphs of exponential functions
Logarithm Functions – In this section we will discuss logarithm functions, evaluation of logarithms and their properties. We will discuss many of the basic manipulations of logarithms that commonly occur in Calculus (and higher) classes. Included is a discussion of the natural ((ln(x))) and common logarithm ((log(x))) as well as the change of base formula.
Exponential and Logarithm Equations – In this section we will discuss various methods for solving equations that involve exponential functions or logarithm functions.
Common Graphs – In this section we will do a very quick review of many of the most common functions and their graphs that typically show up in a Calculus class.

Calculus For Dummies

Limits - In this chapter we introduce the concept of limits. We will discuss the interpretation/meaning of a limit, how to evaluate limits, the definition and evaluation of one-sided limits, evaluation of infinite limits, evaluation of limits at infinity, continuity and the Intermediate Value Theorem. We will also give a brief introduction to a precise definition of the limit and how to use it to evaluate limits

Tangent Lines and Rates of Change – In this section we will introduce two problems that we will see time and again in this course : Rate of Change of a function and Tangent Lines to functions. Both of these problems will be used to introduce the concept of limits, although we won't formally give the definition or notation until the next section.
The Limit – In this section we will introduce the notation of the limit. We will also take a conceptual look at limits and try to get a grasp on just what they are and what they can tell us. We will be estimating the value of limits in this section to help us understand what they tell us. We will actually start computing limits in a couple of sections.
One-Sided Limits – In this section we will introduce the concept of one-sided limits. We will discuss the differences between one-sided limits and limits as well as how they are related to each other.
Limit Properties – In this section we will discuss the properties of limits that we’ll need to use in computing limits (as opposed to estimating them as we've done to this point). We will also compute a couple of basic limits in this section.
Computing Limits – In this section we will looks at several types of limits that require some work before we can use the limit properties to compute them. We will also look at computing limits of piecewise functions and use of the Squeeze Theorem to compute some limits.
Infinite Limits – In this section we will look at limits that have a value of infinity or negative infinity. We’ll also take a brief look at vertical asymptotes.
Limits At Infinity, Part I – In this section we will start looking at limits at infinity, i.e. limits in which the variable gets very large in either the positive or negative sense. We will concentrate on polynomials and rational expressions in this section. We’ll also take a brief look at horizontal asymptotes.
Limits At Infinity, Part II – In this section we will continue covering limits at infinity. We’ll be looking at exponentials, logarithms and inverse tangents in this section.
Continuity – In this section we will introduce the concept of continuity and how it relates to limits. We will also see the Intermediate Value Theorem in this section and how it can be used to determine if functions have solutions in a given interval.
The Definition of the Limit – In this section we will give a precise definition of several of the limits covered in this section. We will work several basic examples illustrating how to use this precise definition to compute a limit. We’ll also give a precise definition of continuity..

Derivatives - In this chapter we introduce Derivatives. We cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well as derivatives of polynomials, roots, trig functions, inverse trig functions, hyperbolic functions, exponential functions and logarithm functions. We also cover implicit differentiation, related rates, higher order derivatives and logarithmic differentiation.

The Definition of the Derivative – In this section we define the derivative, give various notations for the derivative and work a few problems illustrating how to use the definition of the derivative to actually compute the derivative of a function.
Interpretation of the Derivative – In this section we give several of the more important interpretations of the derivative. We discuss the rate of change of a function, the velocity of a moving object and the slope of the tangent line to a graph of a function.
Differentiation Formulas – In this section we give most of the general derivative formulas and properties used when taking the derivative of a function. Examples in this section concentrate mostly on polynomials, roots and more generally variables raised to powers.
Product and Quotient Rule – In this section we will give two of the more important formulas for differentiating functions. We will discuss the Product Rule and the Quotient Rule allowing us to differentiate functions that, up to this point, we were unable to differentiate.
Derivatives of Trig Functions – In this section we will discuss differentiating trig functions. Derivatives of all six trig functions are given and we show the derivation of the derivative of (sin(x)) and (tan(x)).
Derivatives of Exponential and Logarithm Functions – In this section we derive the formulas for the derivatives of the exponential and logarithm functions.
Derivatives of Inverse Trig Functions – In this section we give the derivatives of all six inverse trig functions. We show the derivation of the formulas for inverse sine, inverse cosine and inverse tangent.
Derivatives of Hyperbolic Functions – In this section we define the hyperbolic functions, give the relationships between them and some of the basic facts involving hyperbolic functions. We also give the derivatives of each of the six hyperbolic functions and show the derivation of the formula for hyperbolic sine.
Chain Rule – In this section we discuss one of the more useful and important differentiation formulas, The Chain Rule. With the chain rule in hand we will be able to differentiate a much wider variety of functions. As you will see throughout the rest of your Calculus courses a great many of derivatives you take will involve the chain rule!
Implicit Differentiation – In this section we will discuss implicit differentiation. Not every function can be explicitly written in terms of the independent variable, e.g. y = f(x) and yet we will still need to know what f'(x) is. Implicit differentiation will allow us to find the derivative in these cases. Knowing implicit differentiation will allow us to do one of the more important applications of derivatives, Related Rates (the next section).
Related Rates – In this section we will discuss the only application of derivatives in this section, Related Rates. In related rates problems we are give the rate of change of one quantity in a problem and asked to determine the rate of one (or more) quantities in the problem. This is often one of the more difficult sections for students. We work quite a few problems in this section so hopefully by the end of this section you will get a decent understanding on how these problems work.
Higher Order Derivatives – In this section we define the concept of higher order derivatives and give a quick application of the second order derivative and show how implicit differentiation works for higher order derivatives.
Logarithmic Differentiation – In this section we will discuss logarithmic differentiation. Logarithmic differentiation gives an alternative method for differentiating products and quotients (sometimes easier than using product and quotient rule). More importantly, however, is the fact that logarithm differentiation allows us to differentiate functions that are in the form of one function raised to another function, i.e. there are variables in both the base and exponent of the function.

Applications of Derivatives - In this chapter we will cover many of the major applications of derivatives. Applications included are determining absolute and relative minimum and maximum function values (both with and without constraints), sketching the graph of a function without using a computational aid, determining the Linear Approximation of a function, L’Hospital’s Rule (allowing us to compute some limits we could not prior to this), Newton's Method (allowing us to approximate solutions to equations) as well as a few basic Business applications.

Rates of Change – In this section we review the main application/interpretation of derivatives from the previous chapter (i.e. rates of change) that we will be using in many of the applications in this chapter.
Critical Points – In this section we give the definition of critical points. Critical points will show up in most of the sections in this chapter, so it will be important to understand them and how to find them. We will work a number of examples illustrating how to find them for a wide variety of functions.
Minimum and Maximum Values – In this section we define absolute (or global) minimum and maximum values of a function and relative (or local) minimum and maximum values of a function. It is important to understand the difference between the two types of minimum/maximum (collectively called extrema) values for many of the applications in this chapter and so we use a variety of examples to help with this. We also give the Extreme Value Theorem and Fermat's Theorem, both of which are very important in the many of the applications we'll see in this chapter.
Finding Absolute Extrema – In this section we discuss how to find the absolute (or global) minimum and maximum values of a function. In other words, we will be finding the largest and smallest values that a function will have.
The Shape of a Graph, Part I – In this section we will discuss what the first derivative of a function can tell us about the graph of a function. The first derivative will allow us to identify the relative (or local) minimum and maximum values of a function and where a function will be increasing and decreasing. We will also give the First Derivative test which will allow us to classify critical points as relative minimums, relative maximums or neither a minimum or a maximum.
The Shape of a Graph, Part II – In this section we will discuss what the second derivative of a function can tell us about the graph of a function. The second derivative will allow us to determine where the graph of a function is concave up and concave down. The second derivative will also allow us to identify any inflection points (i.e. where concavity changes) that a function may have. We will also give the Second Derivative Test that will give an alternative method for identifying some critical points (but not all) as relative minimums or relative maximums.
The Mean Value Theorem – In this section we will give Rolle's Theorem and the Mean Value Theorem. With the Mean Value Theorem we will prove a couple of very nice facts, one of which will be very useful in the next chapter.
Optimization Problems – In this section we will be determining the absolute minimum and/or maximum of a function that depends on two variables given some constraint, or relationship, that the two variables must always satisfy. We will discuss several methods for determining the absolute minimum or maximum of the function. Examples in this section tend to center around geometric objects such as squares, boxes, cylinders, etc.
More Optimization Problems – In this section we will continue working optimization problems. The examples in this section tend to be a little more involved and will often involve situations that will be more easily described with a sketch as opposed to the 'simple' geometric objects we looked at in the previous section.
L’Hospital’s Rule and Indeterminate Forms – In this section we will revisit indeterminate forms and limits and take a look at L’Hospital’s Rule. L’Hospital’s Rule will allow us to evaluate some limits we were not able to previously.
Linear Approximations – In this section we discuss using the derivative to compute a linear approximation to a function. We can use the lienar approximation to a function to approximate values of the function at certain points. While it might not seem like a useful thing to do with when we have the function there really are reasons that one might want to do this. We give two ways this can be useful in the examples.
Differentials – In this section we will compute the differential for a function. We will give an application of differentials in this section. However, one of the more important uses of differentials will come in the next chapter and unfortunately we will not be able to discuss it until then.
Newton’s Method – In this section we will discuss Newton's Method. Newton's Method is an application of derivatives will allow us to approximate solutions to an equation. There are many equations that cannot be solved directly and with this method we can get approximations to the solutions to many of those equations.
Business Applications – In this section we will give a cursory discussion of some basic applications of derivatives to the business field. We will revisit finding the maximum and/or minimum function value and we will define the marginal cost function, the average cost, the revenue function, the marginal revenue function and the marginal profit function. Note that this section is only intended to introduce these concepts and not teach you everything about them.

Integrals - In this chapter we will give an introduction to definite and indefinite integrals. We will discuss the definition and properties of each type of integral as well as how to compute them including the Substitution Rule. We will give the Fundamental Theorem of Calculus showing the relationship between derivatives and integrals. We will also discuss the Area Problem, an important interpretation of the definite integral.

Indefinite Integrals – In this section we will start off the chapter with the definition and properties of indefinite integrals. We will not be computing many indefinite integrals in this section. This section is devoted to simply defining what an indefinite integral is and to give many of the properties of the indefinite integral. Actually computing indefinite integrals will start in the next section.
Computing Indefinite Integrals – In this section we will compute some indefinite integrals. The integrals in this section will tend to be those that do not require a lot of manipulation of the function we are integrating in order to actually compute the integral. As we will see starting in the next section many integrals do require some manipulation of the function before we can actually do the integral. We will also take a quick look at an application of indefinite integrals.
Substitution Rule for Indefinite Integrals – In this section we will start using one of the more common and useful integration techniques – The Substitution Rule. With the substitution rule we will be able integrate a wider variety of functions. The integrals in this section will all require some manipulation of the function prior to integrating unlike most of the integrals from the previous section where all we really needed were the basic integration formulas.
More Substitution Rule – In this section we will continue to look at the substitution rule. The problems in this section will tend to be a little more involved than those in the previous section.
Area Problem – In this section we start off with the motivation for definite integrals and give one of the interpretations of definite integrals. We will be approximating the amount of area that lies between a function and the (x)-axis. As we will see in the next section this problem will lead us to the definition of the definite integral and will be one of the main interpretations of the definite integral that we'll be looking at in this material.
Definition of the Definite Integral – In this section we will formally define the definite integral, give many of its properties and discuss a couple of interpretations of the definite integral. We will also look at the first part of the Fundamental Theorem of Calculus which shows the very close relationship between derivatives and integrals
Computing Definite Integrals – In this section we will take a look at the second part of the Fundamental Theorem of Calculus. This will show us how we compute definite integrals without using (the often very unpleasant) definition. The examples in this section can all be done with a basic knowledge of indefinite integrals and will not require the use of the substitution rule. Included in the examples in this section are computing definite integrals of piecewise and absolute value functions.
Substitution Rule for Definite Integrals – In this section we will revisit the substitution rule as it applies to definite integrals. The only real requirements to being able to do the examples in this section are being able to do the substitution rule for indefinite integrals and understanding how to compute definite integrals in general.

Applications of Integrals - In this chapter we will take a look at some applications of integrals. We will look at Average Function Value, Area Between Curves, Volume (both solids of revolution and other solids) and Work.

Average Function Value – In this section we will look at using definite integrals to determine the average value of a function on an interval. We will also give the Mean Value Theorem for Integrals.
Area Between Curves – In this section we’ll take a look at one of the main applications of definite integrals in this chapter. We will determine the area of the region bounded by two curves.
Volumes of Solids of Revolution / Method of Rings – In this section, the first of two sections devoted to finding the volume of a solid of revolution, we will look at the method of rings/disks to find the volume of the object we get by rotating a region bounded by two curves (one of which may be the (x) or (y)-axis) around a vertical or horizontal axis of rotation.
Volumes of Solids of Revolution / Method of Cylinders – In this section, the second of two sections devoted to finding the volume of a solid of revolution, we will look at the method of cylinders/shells to find the volume of the object we get by rotating a region bounded by two curves (one of which may be the (x) or (y)-axis) around a vertical or horizontal axis of rotation.
More Volume Problems – In the previous two sections we looked at solids that could be found by treating them as a solid of revolution. Not all solids can be thought of as solids of revolution and, in fact, not all solids of revolution can be easily dealt with using the methods from the previous two sections. So, in this section we’ll take a look at finding the volume of some solids that are either not solids of revolutions or are not easy to do as a solid of revolution.
Work – In this section we will look at is determining the amount of work required to move an object subject to a force over a given distance.

Also found in: Thesaurus, Medical, Legal, Financial, Acronyms, Idioms, Encyclopedia, Wikipedia.

Related to calculus: integral calculus, differential calculus

cal·cu·lus

(kăl′kyə-ləs)n.pl.cal·cu·li(-lī′) or cal·cu·lus·es

1. Medicine An abnormal concretion in the body, usually formed of mineral salts and found in the gallbladder, kidney, or urinary bladder, for example.

3. Mathematics

a. The branch of mathematics that deals with limits and the differentiation and integration of functions of one or more variables.

b. A method of analysis or calculation using a special symbolic notation.

c. The combined mathematics of differential calculus and integral calculus.

4. A system or method of calculation: '[a] dazzling grasp of the nation's byzantine budget calculus'(David M. Alpern).

[Latin, small stone used in reckoning; see calculate.]

American Heritage® Dictionary of the English Language, Fifth Edition. Copyright © 2016 by Houghton Mifflin Harcourt Publishing Company. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.

calculus

(

ˈkælkjʊləs) n, pl-lusespl-li (

-ˌlaɪ)

1. (Mathematics) a branch of mathematics, developed independently by Newton and Leibniz. Both differential calculus and integral calculus are concerned with the effect on a function of an infinitesimal change in the independent variable as it tends to zero

2. (Mathematics) any mathematical system of calculation involving the use of symbols

3. (Logic) logic an uninterpreted formal system. Compare formal language²

4. (Pathology) pathol a stonelike concretion of minerals and salts found in ducts or hollow organs of the body

[C17: from Latin: pebble, stone used in reckoning, from calx small stone, counter]

Collins English Dictionary – Complete and Unabridged, 12th Edition 2014 © HarperCollins Publishers 1991, 1994, 1998, 2000, 2003, 2006, 2007, 2009, 2011, 2014

cal•cu•lus

(ˈkæl kyə ləs)
n., pl. -li (-ˌlaɪ)
-lus•es.

1. a method of calculation, esp. one of several highly systematic methods of treating problems by a special system of algebraic notations, as differential or integral calculus.

2. a stone, or concretion, formed in the gallbladder, kidney, or other part of the body.

3. a hard, yellowish to brownish black deposit on teeth formed largely through the calcification of dental plaque; tartar.

4. calculation: the calculus of political appeal.

[1610–20; < Latin: pebble, small stone (used in reckoning)]

cal·cu·lus

(kăl′kyə-ləs)

The branch of mathematics that finds the maximum or minimum values of functions by means of differentiation and integration. Calculus can be used to calculate such things as rates of change, the area bounded by curves, and the volume bounded by surfaces. See more at differentiation, integration.

Word History The branch of mathematics called calculus deals with problems that simple arithmetic or algebra cannot deal with, such as finding areas and volumes of unusual shapes and solids, and measuring rates of change. The word calculus comes from the Latin word that means 'little stone, pebble.' How did a word meaning 'little stone' come to refer to this branch of mathematics? The answer comes from the counting practices of the ancient Romans over 2,000 years ago. They would add things up by using little pebbles or stones that represented particular numbers, as on an abacus. Later, the word calculus came to mean not just the pebble used in counting, but a counting system itself. Much more recently, it came to refer to the modern branch of mathematics, which was invented in the 17th century. The word calculus, incidentally, is also the source of the Latin word calculare, 'to add up,' which gives us our word calculate.

The American Heritage® Student Science Dictionary, Second Edition. Copyright © 2014 by Houghton Mifflin Harcourt Publishing Company. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.

calculus

a branch of mathematics that treats the measurement of changing quantities, determining rates of change (differential calculus) and quantities under changing conditions (integral calculus).

calculus

[ˈkælkjʊləs]N (calculuses or calculi (pl)) [ˈkælkjʊlaɪ] (Math) → cálculom
integral/differential calculus → cálculom integral/diferencial

Collins Spanish Dictionary - Complete and Unabridged 8th Edition 2005 © William Collins Sons & Co. Ltd. 1971, 1988 © HarperCollins Publishers 1992, 1993, 1996, 1997, 2000, 2003, 2005

calculus

[ˈkælkjʊləs]n → analysef (mathématique), calculminfinitésimalintegral calculus, differential calculus

calculus

(Math) → Infinitesimalrechnungf, → Differenzialrechnungf, → Differentialrechnungf, → Integralrechnungf

Collins German Dictionary – Complete and Unabridged 7th Edition 2005. © William Collins Sons & Co. Ltd. 1980 © HarperCollins Publishers 1991, 1997, 1999, 2004, 2005, 2007

calculus

[ˈkælkjʊləs]n → calcolo
differential/integral calculus → calcolodifferenziale/integrale

cal·cu·lus

n. cálculo, concreción o pequeña piedra que puede formarse en las secreciones y fluidos del organismo;

calcium oxalate ___ → ___ de oxalato de calcio;

fibrin ___ → ___ de fibrina;

calculus

n (stone) cálculo, piedra; (dent) cálculo, sarro (dental); renal — cálculo renal, piedra en el riñón

Calculus On Teeth

Want to thank TFD for its existence? Tell a friend about us, add a link to this page, or visit the webmaster's page for free fun content.

Calculus Problems

Link to this page:

Noun	1.	calculus - a hard lump produced by the concretion of mineral salts; found in hollow organs or ducts of the body; 'renal calculi can be very painful' bladder stone, cystolith - a calculus formed in the bladder enterolith - a calculus occurring in the intestines bilestone, gallstone - a calculus formed in the gall bladder or its ducts kidney stone, nephrolith, renal calculus, urinary calculus - a calculus formed in the kidney rock, stone - a lump or mass of hard consolidated mineral matter; 'he threw a rock at me' salivary calculus, sialolith - a stone formed in the salivary gland
2.	calculus - an incrustation that forms on the teeth and gums tophus, tartar crust, encrustation, incrustation - a hard outer layer that covers something
3.	calculus - the branch of mathematics that is concerned with limits and with the differentiation and integration of functions math, mathematics, maths - a science (or group of related sciences) dealing with the logic of quantity and shape and arrangement pure mathematics - the branches of mathematics that study and develop the principles of mathematics for their own sake rather than for their immediate usefulness analysis - a branch of mathematics involving calculus and the theory of limits; sequences and series and integration and differentiation differential calculus, method of fluxions - the part of calculus that deals with the variation of a function with respect to changes in the independent variable (or variables) by means of the concepts of derivative and differential integral calculus - the part of calculus that deals with integration and its application in the solution of differential equations and in determining areas or volumes etc. calculus of variations - the calculus of maxima and minima of definite integrals